leetcode刷题B部分

发表于   |   分类于   |     |   阅读次数

目录

[toc]

50. Pow(x, n)（回到目录）

实现 pow(x, n) ，即计算 x 的 n 次幂函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
示例 1:
输入: 2.00000, 10
输出: 1024.00000
示例 2:
输入: 2.10000, 3
输出: 9.26100
示例 3:
输入: 2.00000, -2
输出: 0.25000
解释: 2-2 = 1/22 = 1/4 = 0.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    double myPow(double x, int n) 
    {
        if(n<0) return 1/powxn(x,-n);
        return powxn(x,n);
    }
private:
    double powxn(double x,int n)
    {
        if(n==0) return 1;
        double half=powxn(x,n/2);
        if(n % 2==0)
        {
            return half*half;
        }
        else 
        {
            return half*half*x;
        }
    }
};

54 螺旋矩阵(59)（回到目录）

给定一个包含 m x n 个元素的矩阵（m 行, n 列），请按照顺时针螺旋顺序，返回矩阵中的所有元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
示例 1:
输入:
[
 [ 1, 2, 3 ],
 [ 4, 5, 6 ],
 [ 7, 8, 9 ]
]
输出: [1,2,3,6,9,8,7,4,5]
示例 2:
输入:
[
  [1, 2, 3, 4],
  [5, 6, 7, 8],
  [9,10,11,12]
]
输出: [1,2,3,4,8,12,11,10,9,5,6,7]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) 
    {
        vector<int> res;
        if(matrix.empty()) return res;
        int m=matrix.size();
        int n=matrix[0].size();
        int count=min(m,n)/2;
        int yushu=min(m,n)%2;
        for(int i=0;i<count;i++)
        {
            for(int j=i;j<n-1-i;j++)
            {
                res.push_back(matrix[i][j]);
            }
            for(int j=i;j<m-1-i;j++)
            {
                res.push_back(matrix[j][n-1-i]);
            }
            for(int j=n-1-i;j>=i+1;j--)//这里j>=i+1,不能是j>=i，不然在最左下角的那个元素会重复
            {
                res.push_back(matrix[m-1-i][j]);
            }
            for(int j=m-1-i;j>=i+1;j--)//这里j>=i+1,不能是j>=i，不然在左上角的那个元素会重复
            {
                res.push_back(matrix[j][i]);
            }
        }
        if(yushu==1)
        {
            if(m==n)
            {
                res.push_back(matrix[count][count]);
            }
            else if(m>n)
            {
                for(int i=count;i<m-count;i++)
                {
                    res.push_back(matrix[i][count]);
                }
            }
            else
            {
                for(int i=count;i<n-count;i++)
                {
                    res.push_back(matrix[count][i]);
                }
            }
        }
        return res;
    }
};

58 最后一个单词的长度（回到目录）

给定一个仅包含大小写字母和空格 ‘ ‘ 的字符串，返回其最后一个单词的长度。

如果不存在最后一个单词，请返回 0 。

说明：一个单词是指由字母组成，但不包含任何空格的字符串。

示例:

1
2
输入: "Hello World"
输出: 5

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int lengthOfLastWord(string s) 
    {
        int cnt=0;
        int n=s.size()-1;
        while(s[n]==' ') n--;//
        for(int i=n;i>=0;i--)
        {
            if(s[i] !=' ')
            {
                cnt++;
            }
            else
            {
                break;
            }
        }
        return cnt;
    }
};

59 螺旋矩阵 II(54)（回到目录）

题目描述提示帮助提交记录社区讨论阅读解答
给定一个正整数 n，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。

示例:

1
2
3
4
5
6
7
输入: 3
输出:
[
 [ 1, 2, 3 ],
 [ 8, 9, 4 ],
 [ 7, 6, 5 ]
]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    vector<vector<int>> generateMatrix(int n) 
    {
        vector<vector<int> > matrix(n,vector<int>(n));
        int count=n/2;
        int yushu=n%2;
        int num=1;
        for(int i=0;i<count;i++)
        {
            for(int j=i;j<n-1-i;j++)
            {
                matrix[i][j]=num++;
            }
            for(int j=i;j<n-1-i;j++)
            {
                matrix[j][n-1-i]=num++;
            }
            for(int j=n-1-i;j>=i+1;j--)
            {
                matrix[n-1-i][j]=num++;
            }
            for(int j=n-1-i;j>=i+1;j--)
            {
                matrix[j][i]=num++;;
            }
        }
        if(yushu)
        {
            matrix[count][count]=num++;
        }
        return matrix;
    }
};

62 不同路径（回到目录）

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

例如，上图是一个7 x 3 的网格。有多少可能的路径？

说明：m 和 n 的值均不超过 100。

1
2
3
4
5
6
7
8
9
10
11
12
13
示例 1:
输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右
示例 2:
输入: m = 7, n = 3
输出: 28

方法1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//动态规划
class Solution {
public:
    int uniquePaths(int m, int n) 
    {
        vector<vector<int> >dp(m,vector<int>(n,0));
        for(int i=0;i<m;i++)
        {
            dp[i][0]=1;
        }
        for(int j=0;j<n;j++)
        {
            dp[0][j]=1;
        }
        for(int i=1;i<m;i++)
        {
            for(int j=1;j<n;j++)
            {
                dp[i][j]=dp[i][j-1]+dp[i-1][j];
            }
        }
        return dp[m-1][n-1];
    }
};

方法2

这跟之前那道 Climbing Stairs 爬梯子问题 很类似，那道题是说可以每次能爬一格或两格，问到达顶部的所有不同爬法的个数。而这道题是每次可以向下走或者向右走，求到达最右下角的所有不同走法的个数。那么跟爬梯子问题一样，我们需要用动态规划Dynamic Programming来解，我们可以维护一个二维数组dp，其中dp[i][j]表示到当前位置不同的走法的个数，然后可以得到递推式为:dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，这里为了节省空间，我们使用一维数组dp，一行一行的刷新也可以，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int uniquePaths(int m, int n) 
    {
        vector<int> dp(n,1);
        for(int i=1;i<m;i++)
        {
            for(int j=1;j<n;j++)
            {
                dp[j]=dp[j]+dp[j-1];
            }
        }
        return dp[n-1];
    }
};

63 不同路径 II（回到目录）

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

说明：m 和 n 的值均不超过 100。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
示例 1:
输入:
[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]
输出: 2
解释:
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) 
    {
        if(obstacleGrid.empty() || obstacleGrid[0].empty() || obstacleGrid[0][0]==1)
         {
             return 0;
         }
        int m=obstacleGrid.size();
        int n=obstacleGrid[0].size();
        vector<vector<int> > dp(m,vector<int>(n,0));
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                if(obstacleGrid[i][j]==1)
                {
                    dp[i][j]=0;
                }
                else if(i==0 && j==0)
                {
                    dp[i][j]=1;
                }
                else if(i==0 && j>0)
                {
                    dp[i][j]=dp[i][j-1];
                }
                else if(i>0 && j==0)
                {
                    dp[i][j]=dp[i-1][j];
                }
                else if(i>0 && j>0)
                {
                    dp[i][j]=dp[i][j-1]+dp[i-1][j];
                }
            }
        }
        return dp[m-1][n-1];
    }
};

98. 验证二叉搜索树（回到目录）

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
示例 1:
输入:
    2
   / \
  1   3
输出: true
示例 2:
输入:
    5
   / \
  1   4
     / \
    3   6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
     根节点的值为 5 ，但是其右子节点值为 4 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isValidBST(TreeNode* root) 
    {
        if(root==NULL) return true;
        vector<int> nums;
        inorder(root,nums);
        for(int i=0;i<nums.size()-1;i++)
        {
            if(nums[i+1]<=nums[i])
            {
                return false;
            }
        }
        return true;
    }
private:
    void inorder(TreeNode* root,vector<int> &nums)
    {
        if(!root) return;
        inorder(root->left,nums);
        nums.push_back(root->val);
        inorder(root->right,nums);
    }
};

120 三角形最小路径和（回到目录）

给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。

例如，给定三角形：

1
2
3
4
5
6
[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

使用常规的动态规划解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) 
    {
        vector<vector<int> > dp;
        for(int i=0;i<triangle.size();i++)
        {
            dp.push_back(vector<int>());
            for(int j=0;j<triangle[i].size();j++)
            {
                dp[i].push_back(0);
            }
        }
        for(int j=0;j<dp[dp.size()-1].size();j++)
        {
            dp[dp.size()-1][j]=triangle[dp.size()-1][j];
        }
        
        for(int i=triangle.size()-2;i>=0;i--)
        {
            for(int j=0;j<=triangle[i].size();j++)
            {
                dp[i][j]=min(dp[i+1][j],dp[i+1][j+1])+triangle[i][j];
            }
        }
        return dp[0][0];
    }
};

使用原地覆盖

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) 
    {
        for(int i=triangle.size()-2;i>=0;i--)
        {
            for(int j=0;j<=i;j++)
            {
                triangle[i][j]=min(triangle[i+1][j],triangle[i+1][j+1])+triangle[i][j];
            }
        }
        return triangle[0][0];
    }
};

198 打家劫舍（回到目录）

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。

1
2
3
4
5
6
7
8
9
10
11
12
示例 1:
输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
     偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入: [2,7,9,3,1]
输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
     偷窃到的最高金额 = 2 + 9 + 1 = 12

1
2
3
4
5
6
7
8
9
10
11
12
// 动态规划
class Solution {
public:
    int rob(vector<int> &num) {
        if (num.size() <= 1) return num.empty() ? 0 : num[0];
        vector<int> dp = {num[0], max(num[0], num[1])};
        for (int i = 2; i < num.size(); ++i) {
            dp.push_back(max(num[i] + dp[i - 2], dp[i - 1]));
        }
        return dp.back();
    }
};

213 打家劫舍 II（回到目录）

你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都围成一圈，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。

1
2
3
4
5
6
7
8
9
10
11
示例 1:
输入: [2,3,2]
输出: 3
解释: 你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。
示例 2:
输入: [1,2,3,1]
输出: 4
解释: 你可以先偷窃 1 号房屋（金额 = 1），然后偷窃 3 号房屋（金额 = 3）。
     偷窃到的最高金额 = 1 + 3 = 4 。

在打家劫舍（198）的基础上改动，先去掉第一个，计算一下最高金额，然后只去掉最后一个，计算最高金额。然后比较两种方式的结果，取较大值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {//动态规划
public:
    int rob(vector<int>& nums) 
    {
        if(nums.size()<=1) return nums.empty()? 0: nums[0];
        return max(rob(nums,0,nums.size()-1),rob(nums,1,nums.size()));
    }
private:
    int rob(vector<int> &nums, int start,int end)
    {
        if(end-start<=1) return nums[start];
        vector<int> dp(end,0);
        dp[start]=nums[start];
        dp[start+1]=max(nums[start+1],nums[start]);
        for(int i=start+2;i<end;i++)
        {
            dp[i]=max(dp[i-1],dp[i-2]+nums[i]);
        }
        return dp[dp.size()-1];
    }
};

287 寻找重复数（回到目录）

给定一个包含 n + 1 个整数的数组 nums，其数字都在 1 到 n 之间（包括 1 和n），可知至少存在一个重复的整数。假设只有一个重复的整数，找出这个重复的数。

1
2
3
4
5
6
7
8
9
示例 1:
输入: [1,3,4,2,2]
输出: 2
示例 2:
输入: [3,1,3,4,2]
输出: 3
说明：

不能更改原数组（假设数组是只读的）。
只能使用额外的 O(1) 的空间。
时间复杂度小于 O(n2) 。
数组中只有一个重复的数字，但它可能不止重复出现一次。

分析：这道题和抽屉原理差不多，例如九个抽屉是个钥匙，一定会有一个抽屉是两个要是的。题目要求我们不能改变原数组，即不能给原数组排序，又不能用多余空间，那么哈希表神马的也就不用考虑了，又说时间小于O(n2)，也就不能用brute force的方法，那我们也就只能考虑用二分搜索法了，我们在区别[1, n]中搜索，首先求出中点数mid，然后遍历整个数组，统计所有小于等于mid的个数。如果count 小于等于mid， 说明 1 到 mid 这些数字没有重复项， 重复项在右半边 mid+1 到n， 所以缩小到右半边继续搜索；如果count 大于mid， 说明 1 到 mid 这些数字中有重复项，缩小到 左半边继续搜索。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int findDuplicate(vector<int>& nums) 
    {
        int left=1,right=nums.size()-1;
        while(left<right)
        {
            int mid=(left+right)/2;
            int cnt=0;
            for(auto num:nums)
            {
                if(num<=mid)
                {
                    cnt++;
                }
            }
            if(cnt<=mid) left=mid+1;
            else right=mid;
        }
        return left;
    }
};

303 区域和检索 - 数组不可变（回到目录）

给定一个整数数组 nums，求出数组从索引 i 到 j (i ≤ j) 范围内元素的总和，包含 i, j 两点。

示例：

1
2
3
4
5
给定 nums = [-2, 0, 3, -5, 2, -1]，求和函数为 sumRange()
sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3

说明:

你可以假设数组不可变。
会多次调用 sumRange 方法。
动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class NumArray {
public:
    NumArray(vector<int> nums) 
    {
        dp=nums;
        for(int i=1;i<nums.size();i++)
        {
            dp[i]=dp[i]+dp[i-1];
        }
    }
    
    int sumRange(int i, int j) 
    {
        if(i==0)
        {
            return dp[j];
        }
        else
        {
            return dp[j]-dp[i-1];
        }
    }
private:
    vector<int> dp;
};
/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray obj = new NumArray(nums);
 * int param_1 = obj.sumRange(i,j);
 */

441 排列硬币（回到目录）

你总共有 n 枚硬币，你需要将它们摆成一个阶梯形状，第 k 行就必须正好有 k 枚硬币。

给定一个数字 n，找出可形成完整阶梯行的总行数。

n 是一个非负整数，并且在32位有符号整型的范围内。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
示例 1:
n = 5
硬币可排列成以下几行:
¤
¤ ¤
¤ ¤
因为第三行不完整，所以返回2.
示例 2:
n = 8
硬币可排列成以下几行:
¤
¤ ¤
¤ ¤ ¤
¤ ¤
因为第四行不完整，所以返回3.

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int arrangeCoins(int n) {
        if (n <= 1) return n;
        long low = 1, high = n;
        while (low < high) {
            long mid = low + (high - low) / 2;
            if (mid * (mid + 1) / 2 <= n) low = mid + 1;
            else high = mid;
        }
        return low-1;
    }
};

442 数组中重复的数据（回到目录）

给定一个整数数组 a，其中1 ≤ a[i] ≤ n （n为数组长度）, 其中有些元素出现两次而其他元素出现一次。找到所有出现两次的元素。

你可以不用到任何额外空间并在O(n)时间复杂度内解决这个问题吗？

示例：

1
2
3
4
5
输入:
[4,3,2,7,8,2,3,1]
输出:
[2,3]

使用正负替换法，由于数组中的数字都是在[1，n]区间内，所以，可以数组的元素可以转化成index,将访问过的元素取相反数。如果再次遇到这个数（此时必然是负数了），则将它加入result数组。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    vector<int> findDuplicates(vector<int>& nums) 
    {
        vector<int> res;
        for(int i=0;i<nums.size();i++)
        {
            int index=abs(nums[i])-1;
            if(nums[index]<0) res.push_back(abs(nums[i]));
            nums[index]=-nums[index];
        }
        return res;
    }
};

461 汉明距离（回到目录）

两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。给出两个整数 x 和 y，计算它们之间的汉明距离。

注意：
0 ≤ x, y < 231.

1
2
3
4
5
6
7
8
9
10
11
12
示例:
输入: x = 1, y = 4
输出: 2
解释:
1   (0 0 0 1)
4   (0 1 0 0)
       ↑   ↑
上面的箭头指出了对应二进制位不同的位置。

分析：只要将x和y的二进制形式的每一位取出来按位异或，若为1，则res++,最后的res就是汉明距离。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int hammingDistance(int x, int y) 
    {
        int res=0;
        for(int i=0;i<32;i++)
        {
            if(x&(1<<i)^(y&(1<<i)))
            {
                res++;
            }
        }
        return res;
    }
};

526 优美的排列（回到目录）

假设有从 1 到 N 的 N 个整数，如果从这N个数字中成功构造出一个数组，使得数组的第 i 位 (1 <= i <= N) 满足如下两个条件中的一个，我们就称这个数组为一个优美的排列。

条件：
第 i 位的数字能被 i 整除
i 能被第 i 位上的数字整除
现在给定一个整数 N，请问可以构造多少个优美的排列？

1
2
3
4
5
6
7
8
9
10
11
12
13
示例1:
输入: 2
输出: 2
解释: 
第 1 个优美的排列是 [1, 2]:
  第 1 个位置（i=1）上的数字是1，1能被 i（i=1）整除
  第 2 个位置（i=2）上的数字是2，2能被 i（i=2）整除
第 2 个优美的排列是 [2, 1]:
  第 1 个位置（i=1）上的数字是2，2能被 i（i=1）整除
  第 2 个位置（i=2）上的数字是1，i（i=2）能被 1 整除

说明:
N 是一个正整数，并且不会超过15。

分析：
这道题给了我们1到N，总共N个正数，然后定义了一种优美排列方式，对于该排列中的所有数，如果数字可以整除下标，或者下标可以整除数字，那么我们就是优美排列，让我们求出所有优美排列的个数。那么对于求种类个数，或者是求所有情况，这种问题通常要用递归来做。而递归方法等难点在于写递归函数，如何确定终止条件，还有for循环中变量的起始位置如何确定。那么这里我们需要一个visited数组来记录数字是否已经访问过，因为优美排列中不能有重复数字。我们用变量pos来标记已经生成的数字的个数，如果大于N了，说明已经找到了一组排列，结果res自增1。在for循环中，i应该从1开始，因为我们遍历1到N中的所有数字，如果该数字未被使用过，且满足和坐标之间的整除关系，那么我们标记该数字已被访问过，再调用下一个位置的递归函数，之后不要忘记了恢复初始状态。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//递归方法
class Solution {
public:
    int countArrangement(int N) {
        int res = 0;
        vector<int> visited(N + 1, 0);
        dfs(N, visited, 1, res);
        return res;
    }
    void dfs(int N, vector<int>& visited, int pos, int& res) {
        if (pos > N) {
            ++res; 
            return;
        }
//for里面的代码是指某个数字都放在每个位置一次
        for (int i = 1; i <= N; ++i) {
            if (visited[i] == 0 && (i % pos == 0 || pos % i == 0)) {
                visited[i] = 1;
                dfs(N, visited, pos + 1, res);
                visited[i] = 0;
            }
        }
    }
};

667 优美的排列 II（回到目录）

定两个整数 n 和 k，你需要实现一个数组，这个数组包含从 1 到 n 的 n 个不同整数，同时满足以下条件：

① 如果这个数组是 [a1, a2, a3, … , an] ，那么数组 [|a1 - a2|, |a2 - a3|, |a3 - a4|, … , |an-1 - an|] 中应该有且仅有 k 个不同整数；.

② 如果存在多种答案，你只需实现并返回其中任意一种.

1
2
3
4
5
6
7
8
9
10
11
12
示例 1:
输入: n = 3, k = 1
输出: [1, 2, 3]
解释: [1, 2, 3] 包含 3 个范围在 1-3 的不同整数， 并且 [1, 1] 中有且仅有 1 个不同整数 : 1
 
示例 2:
输入: n = 3, k = 2
输出: [1, 3, 2]
解释: [1, 3, 2] 包含 3 个范围在 1-3 的不同整数， 并且 [2, 1] 中有且仅有 2 个不同整数: 1 和 2

提示:
n 和 k 满足条件 1 <= k < n <= 104.

分析：这题的意思是给出1到n的不同整数，求k种不同相邻数的绝对值差值情况下的排列（任意一种即可）。
其实，k的最大值是n-1，使用最小最大相邻就可以了。

  • 如果给出n=4,k=2,则ans=[4,1,2,3]，也就是说，把最大数放在最小数之前，k自动减1，当k减到1时，之后的数按升序排列，就是两种排法了。

  • 如果给出n=4,k=3,则ans=[1,4,2,3],把最大数依次插入在最小的数之后，当k减到1时，之后的数依次按升序排列。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
     class Solution {
    public:
        vector<int> constructArray(int n, int k) 
        {
            vector<int> res;
            int i=1,j=n;
            while(i<=j)
            {
                if(k>1)
                {
                    if(k%2)
                    {
                        res.push_back(i);
                        i++;
                    }
                    else
                    {
                        res.push_back(j);
                        j--;
                    }
                    k--;
                }
                else
                {
                    res.push_back(i);
                    i++;
                }
            }
            return res;
        }
    };

简化版的代码

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    vector<int> constructArray(int n, int k) {
        vector<int> res;
        int i = 1, j = n;
        while (i <= j) {
            if (k > 1) res.push_back(k-- % 2 ? i++ : j--);
            else res.push_back(i++);
        }
        return res;
    }
};

283 移动零（回到目录）

题目描述提示帮助提交记录社区讨论阅读解答
给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

示例:

1
2
输入: [0,1,0,3,12]
输出: [1,3,12,0,0]

说明:

  • 必须在原数组上操作，不能拷贝额外的数组。
  • 尽量减少操作次数。

分析：这道题很简单，使用双指针i和j，同时指向0。其中i用于扫描nums数组的每一个元素，遇到非零的元素，就和nums[j]交换，然后j++。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {//双指针
public:
    void moveZeroes(vector<int>& nums) 
    {
        for(int i=0,j=0;i<nums.size();i++)
        {
            if(nums[i]!=0)
            {
                swap(nums[i],nums[j]);
                j++;
            }
        }
    }
};

605 种花问题（回到目录）

假设你有一个很长的花坛，一部分地块种植了花，另一部分却没有。可是，花卉不能种植在相邻的地块上，它们会争夺水源，两者都会死去。

给定一个花坛（表示为一个数组包含0和1，其中0表示没种植花，1表示种植了花），和一个数 n 。能否在不打破种植规则的情况下种入 n 朵花？能则返回True，不能则返回False。

1
2
3
4
5
6
7
8
示例 1:
输入: flowerbed = [1,0,0,0,1], n = 1
输出: True
示例 2:
输入: flowerbed = [1,0,0,0,1], n = 2
输出: False

注意:数组内已种好的花不会违反种植规则。
输入的数组长度范围为 [1, 20000]。
n 是非负整数，且不会超过输入数组的大小。

分析：对于连续的0来说，主要是考虑边界问题。例如000，如果是放在边界，则101，即种2盆花；如果两边是1，就只能放1盆(010)。所以这里有个技巧是，若两边是0，则直接插入一个0，这样，原来的边界处就可以放心的种花了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    bool canPlaceFlowers(vector<int>& flowerbed, int n) 
    {
        if(flowerbed[0]==0) flowerbed.insert(flowerbed.begin(),0);
        if(flowerbed.back()==0) flowerbed.push_back(0);
        int len=flowerbed.size();
        int cnt=0,sum=0;
        for(int i=0;i<=len;i++)
        {
            if(i<len && flowerbed[i]==0)
            {
                cnt++;
            }
            else
            {
                sum +=(cnt-1)/2;
                cnt=0;
            }
        }
        return sum>=n;
    }
};

643 子数组最大平均数 I（回到目录）

给定 n 个整数，找出平均数最大且长度为 k 的连续子数组，并输出该最大平均数。

示例 1:

1
2
3
输入: [1,12,-5,-6,50,3], k = 4
输出: 12.75
解释: 最大平均数 (12-5-6+50)/4 = 51/4 = 12.75

注意:

1
2
1 <= k <= n <= 30,000。
所给数据范围 [-10,000，10,000]。

分析：这道题，我的思路比较暴力，直接计算每个k元组元素的和，计算出最大的那个。然后得到平均数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    double findMaxAverage(vector<int>& nums, int k) 
    {
        int len=nums.size();
        if(len==1) return nums[0];
        vector<int> sum(len,0);
        sum[0]=nums[0];
        for(int i=1;i<len;i++)
        {
            sum[i]=sum[i-1]+nums[i];
        }
        double max_sum=sum[k-1];
        for(int i=k;i<len;i++)
        {
            double temp=sum[i]-sum[i-k];
            max_sum=max(temp,max_sum);
        }
        return max_sum/k;
    }
};

665 非递减数列（回到目录）

给定一个长度为 n 的整数数组，你的任务是判断在最多改变 1 个元素的情况下，该数组能否变成一个非递减数列。

我们是这样定义一个非递减数列的： 对于数组中所有的 i (1 <= i < n)，满足 array[i] <= array[i + 1]。

1
2
3
4
5
6
7
8
9
10
示例 1:
输入: [4,2,3]
输出: True
解释: 你可以通过把第一个4变成1来使得它成为一个非递减数列。
示例 2:
输入: [4,2,1]
输出: False
解释: 你不能在只改变一个元素的情况下将其变为非递减数列。

说明: n 的范围为 [1, 10,000]。
分析：这道题给了我们一个数组，说我们最多有1次修改某个数字的机会，问能不能将数组变为非递减数组。题目中给的例子太少，不能覆盖所有情况，我们再来看下面三个例子：

1
2
3
4
5
4，2，3
-1，4，2，3
2，3，3，2，4

我们通过分析上面三个例子可以发现，当我们发现后面的数字小于前面的数字产生冲突后，有时候需要修改前面较大的数字(比如前两个例子需要修改4)，有时候却要修改后面较小的那个数字(比如前第三个例子需要修改2)，那么有什么内在规律吗？是有的，判断修改那个数字其实跟再前面一个数的大小有关系，首先如果再前面的数不存在，比如例子1，4前面没有数字了，我们直接修改前面的数字为当前的数字2即可。而当再前面的数字存在，并且小于当前数时，比如例子2，-1小于2，我们还是需要修改前面的数字4为当前数字2；如果再前面的数大于当前数，比如例子3，3大于2，我们需要修改当前数2为前面的数3。这是修改的情况，由于我们只有一次修改的机会，所以用一个变量cnt，初始化为1，修改数字后cnt自减1，当下次再需要修改时，如果cnt已经为0了，直接返回false。遍历结束后返回true。

修改的原则：尽量使把数字往小的改。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    bool checkPossibility(vector<int>& nums) 
    {
        int cnt=1;
        for(int i=1;i<nums.size();i++)
        {
            if(nums[i]<nums[i-1])
            {
                if(cnt==0) return false;
                if(i==1 || nums[i]>=nums[i-2]) nums[i-1]=nums[i];
                else
                {
                    nums[i]=nums[i-1];
                }
                cnt--;
            }
        }
        return true;
    }
};

131 分割回文串（回到目录）

给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。

返回 s 所有可能的分割方案。

示例:

1
2
3
4
5
6
输入: "aab"
输出:
[
  ["aa","b"],
  ["a","a","b"]
]

这是一道需要用DFS来解的题目，既然题目要求找到所有可能拆分成回文数的情况，那么肯定是所有的情况都要遍历到，对于每一个子字符串都要分别判断一次是不是回文数，那么肯定有一个判断回文数的子函数，还需要一个DFS函数用来递归，再加上原本的这个函数，总共需要三个函数来求解。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {//循环里有递归
public:
    vector<vector<string>> partition(string s) {
        vector<vector<string>> res;
        vector<string> out;
        partitionDFS(s, 0, out, res);
        return res;
    }
    void partitionDFS(string s, int start, vector<string> &out, vector<vector<string>> &res) {
        if (start == s.size()) {
            res.push_back(out);
            return;
        }
        for (int i = start; i < s.size(); ++i) {
            if (isPalindrome(s, start, i)) {
                out.push_back(s.substr(start, i - start + 1));
                partitionDFS(s, i + 1, out, res);
                out.pop_back();
            }
        }
    }
    bool isPalindrome(string s, int start, int end) {
        while (start < end) {
            if (s[start] != s[end]) return false;
            ++start;
            --end;
        }
        return true;
    }
};

注：那么，对原字符串的所有子字符串的访问顺序是什么呢，如果原字符串是 abcd, 那么访问顺序为:a -> b -> c -> d -> cd -> bc -> bcd-> ab -> abc -> abcd, 这是对于没有两个或两个以上子回文串的情况。那么假如原字符串是aabc，那么访问顺序为：a -> a -> b -> c -> bc -> ab -> abc -> aa -> b -> c -> bc -> aab -> aabc，中间当检测到aa时候，发现是回文串，那么对于剩下的bc当做一个新串来检测，于是有b -> c -> bc，这样扫描了所有情况，即可得出最终答案。

股票问题

121 买卖股票的最佳时机（回到目录）

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。

注意你不能在买入股票前卖出股票。

1
2
3
4
5
6
7
8
9
10
11
示例 1:
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
示例 2:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

引入两个变量，最小买入价格和最大利润，遍历数组，判断最大和最小值来得到最后的结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int maxProfit(vector<int>& prices) 
    {
        /*
        vector<pair<int> > stock;
        for(int i=1;i<=prices.size();i++)
        {
            stock.push_back(make_pair(i,prices[i]));
        }
        */
        if(prices.size()<=1) return 0;
        int max_pro=0;
        int temp_min=prices[0];
        int len=prices.size();
        for(int i=1;i<len;i++)
        {
            temp_min=min(temp_min,prices[i]);
            max_pro=max(max_pro,prices[i]-temp_min);
        }
        return max_pro;
    }
};

122 买卖股票的最佳时机 II（回到目录）

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
示例 1:
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
     随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
     注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。
     因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。
示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

分析：炒股想挣钱当然是低价买入高价抛出，那么这里我们只需要从第二天开始，如果当前价格比之前价格高，则把差值加入利润中，因为我们可以昨天买入，今日卖出，若明日价更高的话，还可以今日买入，明日再抛出。以此类推，遍历完整个数组后即可求得最大利润。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int maxProfit(vector<int>& prices) 
    {
        int len=prices.size();
        int res=0;
        for(int i=0;i<len-1;i++)
        {
            if(prices[i]<prices[i+1])
            {
                res +=prices[i+1]-prices[i];
            }
        }
        return res;
    }
};

说明：其他几个股票问题有点难，现在不想做了

516 最长回文子序列（回到目录）

给定一个字符串s，找到其中最长的回文子序列。可以假设s的最大长度为1000。

1
2
3
4
5
6
7
8
9
示例 1:
输入:"bbbab"
输出:4
一个可能的最长回文子序列为 "bbbb"。
示例 2:
输入:"cbbd"
输出:2
一个可能的最长回文子序列为 "bb"。

这道题给了我们一个字符串，让我们求最大的回文子序列，子序列和子字符串不同，不需要连续。而关于回文串的题之前也做了不少，处理方法上就是老老实实的两两比较吧。像这种有关极值的问题，最应该优先考虑的就是贪婪算法和动态规划，这道题显然使用DP更加合适。我们建立一个二维的DP数组，其中dp[i][j]表示[i,j]区间内的字符串的最长回文子序列，那么对于递推公式我们分析一下，如果s[i]==s[j]，那么i和j就可以增加2个回文串的长度，我们知道中间dp[i + 1][j - 1]的值，那么其加上2就是dp[i][j]的值。如果s[i] != s[j]，那么我们可以去掉i或j其中的一个字符，然后比较两种情况下所剩的字符串谁dp值大，就赋给dp[i][j]，那么递推公式如下：

1
2
3
4
5
              /  dp[i + 1][j - 1] + 2                       if (s[i] == s[j])
dp[i][j] =
              \  max(dp[i + 1][j], dp[i][j - 1])        if (s[i] != s[j])

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {//动态规划
public:
    int longestPalindromeSubseq(string s) {
        int n = s.length();
        vector<vector<int>> dp(n, vector<int>(n, 0));
        
        for (int i = 0; i < n; i++)
            dp[i][i] = 1;
        
        for (int j = 1; j < n; j++)             // 子串结束位置
            for (int i = j-1; i >=0; i--) {     // 子串开始位置
                if (s[i] == s[j])
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                else
                    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
            }
        return dp[0][n - 1];
    }
};


74 搜索二维矩阵

编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
示例 1:
输入:
matrix = [
  [1,   3,  5,  7],
  [10, 11, 16, 20],
  [23, 30, 34, 50]
]
target = 3
输出: true
示例 2:
输入:
matrix = [
  [1,   3,  5,  7],
  [10, 11, 16, 20],
  [23, 30, 34, 50]
]
target = 13
输出: false

这段代码里用到了两次二分查找，两次查找的代码模板不一样。
这道题要求搜索一个二维矩阵，由于给的矩阵是有序的，所以很自然的想到要用二分查找法，我们可以在第一列上先用一次二分查找法找到目标值所在的行的位置，然后在该行上再用一次二分查找法来找是否存在目标值，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 二分查找法
class Solution {
public:
    bool searchMatrix(vector<vector<int> > &matrix, int target) {
        if (matrix.empty() || matrix[0].empty()) return false;
        if (target < matrix[0][0] || target > matrix.back().back()) return false;
        int left = 0, right = matrix.size();
        while (left < right) {
            int mid = (left + right) / 2;
            if (matrix[mid][0] == target) return true;
            else if (matrix[mid][0] < target) left = mid + 1;
            else right = mid;
        }
        int tmp = right-1;
        
        left = 0;
        right = matrix[tmp].size() - 1;
        while (left <= right) {
            int mid = (left + right) / 2;
            if (matrix[tmp][mid] == target) return true;
            else if (matrix[tmp][mid] < target) left = mid + 1;
            else right = mid - 1;
        }
        return false;
    }
};

240 搜索二维矩阵 II

题目描述提示帮助提交记录社区讨论阅读解答
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
示例:

1
2
3
4
5
6
7
8
9
10
11
12
现有矩阵 matrix 如下：
[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]
给定 target = 5，返回 true。
给定 target = 20，返回 false。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) 
    {
        if(matrix.size()==0 || matrix[0].size()==0) return false;
        int m=matrix.size()-1,n=matrix[0].size()-1;
        if(target<matrix[0][0] || target>matrix[m][n]) return false;
        int x=m,y=0;
        while(1)
        {
            if(target>matrix[x][y]) y++;
            else if(target<matrix[x][y]) x--;
            else return true;
            if(x<0 || y>n) break;
        }
        return false;
    }
};

107 二叉树的层次遍历 II

给定一个二叉树，返回其节点值自底向上的层次遍历。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
例如：
给定二叉树 [3,9,20,null,null,15,7],
    3
   / \
  9  20
    /  \
   15   7
返回其自底向上的层次遍历为：
[
  [15,7],
  [9,20],
  [3]
]

递归方式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) 
    {
        vector<vector<int> > res;
        recursive(0,res,root);
        return vector<vector<int> > (res.rbegin(),res.rend());
    }
    void recursive(int level,vector<vector<int> > &res,TreeNode* root)
    {
        if(root==NULL) return;
        if(level==res.size()) res.push_back({});
        res[level].push_back(root->val);
        recursive(level+1,res,root->left);
        recursive(level+1,res,root->right);
    }
};

迭代方式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) 
    {
        vector<vector<int> > res;
        if(root==NULL) return res;
        queue<TreeNode*> q;
        q.push(root);
        while(!q.empty())
        {
            vector<int> level;
            TreeNode* node=NULL;
            int len=q.size();
            for(int i=0;i<len;i++)
            {
                node=q.front();
                level.push_back(node->val);
                q.pop();
                if(node->left) q.push(node->left);
                if(node->right) q.push(node->right);
            }
            res.insert(res.begin(),level);
        }
        return res;
    }
};

344 反转字符串

编写一个函数，其作用是将输入的字符串反转过来。

1
2
3
4
5
6
7
8
示例 1:
输入: "hello"
输出: "olleh"
示例 2:
输入: "A man, a plan, a canal: Panama"
输出: "amanaP :lanac a ,nalp a ,nam A"

我的解法

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    string reverseString(string s) 
    {
        string res;
        for(int i=s.size()-1;i>=0;i--)
        {
            res.push_back(s[i]);
        }
        return res;
    }
};

参考解法

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    string reverseString(string s) 
    {
        int i=0,j=s.size()-1;
        while(i<j)
        {
            swap(s[i++],s[j--]);
        }
        return s;
    }
};

349 两个数组的交集

给定两个数组，编写一个函数来计算它们的交集。

1
2
3
4
5
6
7
8
示例 1:
输入: nums1 = [1,2,2,1], nums2 = [2,2]
输出: [2]
示例 2:
输入: nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出: [9,4]

说明:

  • 输出结果中的每个元素一定是唯一的。
  • 我们可以不考虑输出结果的顺序。

method1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) 
    {
        if(nums1.empty() || nums2.empty()) return vector<int> ();
        set<int> s(nums1.begin(),nums1.end()),res;
        for(auto num:nums2)
        {
            if(s.count(num))
            {
                res.insert(num);
            }
        }
        return vector<int>(res.begin(),res.end());
    }
};

method2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) 
    {
        if(nums1.empty() || nums2.empty()) return vector<int> ();
        set<int> res;
        int i=0,j=0;
        sort(nums1.begin(),nums1.end());
        sort(nums2.begin(),nums2.end());
        while(i< nums1.size() && j<nums2.size())
        {
            if(nums1[i]==nums2[j])
            {
                res.insert(nums1[i]);
                i++;j++;
            }
            else if(nums1[i]<nums2[j])
            {
                i++;
            }
            else
            {
                j++;
            }
        }
        return vector<int> (res.begin(),res.end());
    }
};
`

350 两个数组的交集 II

给定两个数组，编写一个函数来计算它们的交集。

1
2
3
4
5
6
7
8
9
10
11
12
示例 1:
输入: nums1 = [1,2,2,1], nums2 = [2,2]
输出: [2,2]
示例 2:
输入: nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出: [4,9]
说明：
输出结果中每个元素出现的次数，应与元素在两个数组中出现的次数一致。
我们可以不考虑输出结果的顺序。

进阶:

  • 如果给定的数组已经排好序呢？你将如何优化你的算法？
  • 如果 nums1 的大小比 nums2 小很多，哪种方法更优？
  • 如果 nums2 的元素存储在磁盘上，磁盘内存是有限的，并且你不能一次加载所有的元素到内存中，你该怎么办？

解法1

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2) 
    {
        map<int, int> m;
        vector<int> res;
        for (auto a : nums1) ++m[a];
        for (auto a : nums2) {
            if (m[a]-- > 0) res.push_back(a);
        }
        return res;
    }
};

解法2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
        vector<int> res;
        int i = 0, j = 0;
        sort(nums1.begin(), nums1.end());
        sort(nums2.begin(), nums2.end());
        while (i < nums1.size() && j < nums2.size()) {
            if (nums1[i] == nums2[j]) {
                res.push_back(nums1[i]);
                ++i; ++j;
            } else if (nums1[i] > nums2[j]) {
                ++j;
            } else {
                ++i;
            }
        }
        return res;
    }
};

788 旋转数字

我们称一个数 X 为好数, 如果它的每位数字逐个地被旋转 180 度后，我们仍可以得到一个有效的，且和 X 不同的数。要求每位数字都要被旋转。

如果一个数的每位数字被旋转以后仍然还是一个数字， 则这个数是有效的。0, 1, 和 8 被旋转后仍然是它们自己；2 和 5 可以互相旋转成对方；6 和 9 同理，除了这些以外其他的数字旋转以后都不再是有效的数字。

现在我们有一个正整数 N, 计算从 1 到 N 中有多少个数 X 是好数？

1
2
3
4
5
6
7
示例:
输入: 10
输出: 4
解释: 
在[1, 10]中有四个好数： 2, 5, 6, 9。
注意 1 和 10 不是好数, 因为他们在旋转之后不变。
注意:

N 的取值范围是 [1, 10000]。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int rotatedDigits(int N) 
    {
        int res=0;
        for(int i=0;i<=N;i++)
        {
            if(check(i))
            {
                res++;
            }
        }
        return res;
    }
    bool check(int n)
    {
        string str=to_string(n);
        bool flag=false;
        for(auto c:str)
        {
            if(c=='3' || c=='4' || c=='7') return false;
            if(c=='2' || c=='5' || c=='6' || c=='9') flag=true;
        }
        return flag;
    }
};

796 旋转字符串

给定两个字符串, A 和 B。

A 的旋转操作就是将 A 最左边的字符移动到最右边。 例如, 若 A = ‘abcde’，在移动一次之后结果就是’bcdea’ 。如果在若干次旋转操作之后，A 能变成B，那么返回True。

1
2
3
4
5
6
7
8
示例 1:
输入: A = 'abcde', B = 'cdeab'
输出: true
示例 2:
输入: A = 'abcde', B = 'abced'
输出: false
注意：

A 和 B 长度不超过 100。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    bool rotateString(string A, string B) 
    {
        if(A.size()==0 && B.size()==0) return true;
        if(A.size()!=B.size()) return false;
        for(int i=0;i<A.size();i++)
        {
            if(A.substr(i,A.size()-i)+A.substr(0,i) == B) return true;
        }
        return false;
    }
};

804 唯一摩尔斯密码词

国际摩尔斯密码定义一种标准编码方式，将每个字母对应于一个由一系列点和短线组成的字符串， 比如: “a” 对应 “.-“, “b” 对应 “-…”, “c” 对应 “-.-.”, 等等。

为了方便，所有26个英文字母对应摩尔斯密码表如下：

[".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."]

给定一个单词列表，每个单词可以写成每个字母对应摩尔斯密码的组合。例如，”cab” 可以写成 “-.-.-….-“，(即 “-.-.” + “-…” + “.-“字符串的结合)。我们将这样一个连接过程称作单词翻译。

返回我们可以获得所有词不同单词翻译的数量。

1
2
3
4
5
6
7
8
9
10
11
例如:
输入: words = ["gin", "zen", "gig", "msg"]
输出: 2
解释: 
各单词翻译如下:
"gin" -> "--...-."
"zen" -> "--...-."
"gig" -> "--...--."
"msg" -> "--...--."
共有 2 种不同翻译, "--...-." 和 "--...--.".

注意:

  • 单词列表words 的长度不会超过 100。
  • 每个单词 words[i]的长度范围为 [1, 12]。
  • 每个单词 words[i]只包含小写字母。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int uniqueMorseRepresentations(vector<string>& words) 
    {
        vector<string> morse{".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."};
        set<string> res;
        for(auto word:words)
        {
            string temp="";
            for(char c:word)
            {
                temp=temp+morse[c-'a'];
            }
            res.insert(temp);
        }
        return res.size();
    }
};

371 两整数之和

题目描述提示帮助提交记录社区讨论阅读解答
不使用运算符 + 和-，计算两整数a 、b之和。

示例：
若 a = 1 ，b = 2，返回 3。

使用位运算的方法：我们在做加法运算的时候，每位相加之后可能会有进位Carry产生，然后在下一位计算时需要加上进位一起运算，那么我们能不能将两部分拆开呢，我们来看一个例子759+674

  1. 如果我们不考虑进位，可以得到323

  2. 如果我们只考虑进位，可以得到1110

  3. 我们把上面两个数字假期323+1110=1433就是最终结果了

然后我们进一步分析，如果得到上面的第一第二种情况，我们在二进制下来看，不考虑进位的加，0+0=0， 0+1=1, 1+0=1， 1+1=0，这就是异或的运算规则，如果只考虑进位的加0+0=0, 0+1=0, 1+0=0, 1+1=1，而这其实这就是与的运算，而第三步在将两者相加时，我们再递归调用这个算法，终止条件是当进位为0时，我们直接返回第一步的结果，参见代码如下：

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    int getSum(int a, int b) 
    {
        if(b==0) return a;
        int sum=a^b;
        int carry=(a&b)<<1;
        return getSum(sum,carry);
    }
};

迭代法：

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int getSum(int a, int b) {
        while (b) {
            int carry = (a & b) << 1;
            a = a ^ b;
            b = carry;
        }
        return a;
    }
};

172 阶乘后的零

给定一个整数 n，返回 n! 结果尾数中零的数量。

1
2
3
4
5
6
7
8
9
10
示例 1:
输入: 3
输出: 0
解释: 3! = 6, 尾数中没有零。
示例 2:
输入: 5
输出: 1
解释: 5! = 120, 尾数中有 1 个零.

说明: 你算法的时间复杂度应为 O(log n) 。
分析：这道题是求一个数的阶乘末尾0的个数，也就是要找乘数中10的个数，而10可分解为2和5，而我们可知2的数量又远大于5的数量，那么此题只需要找出5的个数。仍需注意的一点就是，像25,125，这样的不只含有一个5的数字需要考虑进去。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int trailingZeroes(int n) 
    {
        int res=0;
        while(n)
        {
            res +=n/5;
            n=n/5;
        }
        return res;
    }
};

235 二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
例如，给定如下二叉搜索树:  root = [6,2,8,0,4,7,9,null,null,3,5]
        _______6______
       /              \
    ___2__          ___8__
   /      \        /      \
   0      _4       7       9
         /  \
         3   5
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

  • 所有节点的值都是唯一的。
  • p、q 为不同节点且均存在于给定的二叉搜索树中。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) 
    {
        TreeNode* res=NULL;
        vector<TreeNode*> path;
        vector<TreeNode*> path_p;
        vector<TreeNode*> path_q;
        int flag=0;
        preorder(root,p,path,path_p,flag);
        path.clear();
        flag=0;
        preorder(root,q,path,path_q,flag);
        int min_length=min(path_p.size(),path_q.size());
        for(int i=0;i<min_length;i++)
        {
            if(path_p[i]==path_q[i])//妈的，一开始这行代码多了一个;不报语法错！！！
            {
                res=path_p[i];
            }
        }
        return res;
    }
private:
    void preorder(TreeNode* root,TreeNode* node,vector<TreeNode*> &path,vector<TreeNode*> &res,int flag)
    {
        //vector<TreeNode*> path;//不能把path放在这里，要从外面传进来
        //int flag=0;//这个变量也是，要从外面进来
        if(root==NULL || flag) return;
        path.push_back(root);
        if(root==node) 
        {
            res=path;
            flag=1;
        }
        preorder(root->left,node,path,res,flag);
        preorder(root->right,node,path,res,flag);
        path.pop_back();
    }
};

236 二叉树的最近公共祖先

代码同235

661 图片平滑器

包含整数的二维矩阵 M 表示一个图片的灰度。你需要设计一个平滑器来让每一个单元的灰度成为平均灰度 (向下舍入) ，平均灰度的计算是周围的8个单元和它本身的值求平均，如果周围的单元格不足八个，则尽可能多的利用它们。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
示例 1:
输入:
[[1,1,1],
 [1,0,1],
 [1,1,1]]
输出:
[[0, 0, 0],
 [0, 0, 0],
 [0, 0, 0]]
解释:
对于点 (0,0), (0,2), (2,0), (2,2): 平均(3/4) = 平均(0.75) = 0
对于点 (0,1), (1,0), (1,2), (2,1): 平均(5/6) = 平均(0.83333333) = 0
对于点 (1,1): 平均(8/9) = 平均(0.88888889) = 0

注意:

  • 给定矩阵中的整数范围为 [0, 255]。
  • 矩阵的长和宽的范围均为 [1, 150]。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    vector<vector<int>> imageSmoother(vector<vector<int>>& M) 
    {   
        if(M.size()==0 || M[0].size()==0) return M;
        vector<vector<int> > dirs={{-1,0},{1,0},{0,-1},{0,1},{-1,-1},{-1,1},{1,-1},{1,1}};
        int m=M.size();
        int n=M[0].size();
        vector<vector<int> > res(m,vector<int>(n,0));
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                int sum=M[i][j];
                int cnt=1;
                for(auto dir:dirs)
                {
                    int x=i+dir[0];
                    int y=j+dir[1];
                    if(x<0 || x>=m || y<0 || y>=n) continue;
                    cnt++;
                    sum=sum+M[x][y];
                }
                res[i][j]=sum/cnt;
            }
        }
        return res;
    }
};

217 存在重复元素

给定一个整数数组，判断是否存在重复元素。

如果任何值在数组中出现至少两次，函数返回 true。如果数组中每个元素都不相同，则返回 false。

1
2
3
4
5
6
7
8
9
10
11
12
示例 1:
输入: [1,2,3,1]
输出: true
示例 2:
输入: [1,2,3,4]
输出: false
示例 3:
输入: [1,1,1,3,3,4,3,2,4,2]
输出: true

代码：一看到题目（和 389 找不同 类似的思路）就写出来了代码，我的思路非常简单。使用map记录每个元素出现的次数，然后每个元素的次数都-1，再判断该元素的次数是否>0，若是，则返回true。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    bool containsDuplicate(vector<int>& nums) 
    {
        map<int,int> m;
        for(int i=0;i<nums.size();i++)
        {
            m[nums[i]]++;
        }
        for(int i=0;i<nums.size();i++)
        {
            if(--m[nums[i]] >0)
            {
                return true;
            }
        }
        return false;
    }
};

219 存在重复元素 II

给定一个整数数组和一个整数 k，判断数组中是否存在两个不同的索引 i 和 j，使得 nums [i] = nums [j]，并且 i 和 j 的差的绝对值最大为 k。

1
2
3
4
5
6
7
8
9
10
11
12
示例 1:
输入: nums = [1,2,3,1], k = 3
输出: true
示例 2:
输入: nums = [1,0,1,1], k = 1
输出: true
示例 3:
输入: nums = [1,2,3,1,2,3], k = 2
输出: false

首先定义一个pair的vector,目的是绑定元素和它对应的index,r然后进行元素大小排列，先判断两个元素相等时候，index之差是否<=k，如果是，就返回true.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
bool cmp(pair<int,int> &a,pair<int,int> &b)//cmp函数应该定义在类外面
    {
        return a.first<b.first;
    }
class Solution {
public:
    bool containsNearbyDuplicate(vector<int>& nums, int k) 
    {
        int len=nums.size();
        vector<pair<int,int> >t;
        for(int i=0;i<len;i++)
        {
            t.push_back(make_pair(nums[i],i));
        }
        sort(t.begin(),t.end(),cmp);
        for(int i=0;i<len;i++)
        {
            int j=i+1;
            while(t[i].first==t[j].first && j<len)
            {
                if(abs(t[i].second-t[j].second)<=k)
                    return true;
                j++;
            }
        }
        return false;
    }  
};

220 存在重复元素 III

给定一个整数数组，判断数组中是否有两个不同的索引 i 和 j，使得 nums [i] 和 nums [j] 的差的绝对值最大为 t，并且 i 和 j 之间的差的绝对值最大为 ķ。

1
2
3
4
5
6
7
8
9
10
11
12
示例 1:
输入: nums = [1,2,3,1], k = 3, t = 0
输出: true
示例 2:
输入: nums = [1,0,1,1], k = 1, t = 2
输出: true
示例 3:
输入: nums = [1,5,9,1,5,9], k = 2, t = 3
输出: false

和上一题的代码基本类似

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
bool cmp(pair<long,long> &a,pair<long,long> &b)//cmp函数应该定义在类外面
    {
        return a.first<b.first;
    }
class Solution {
public:
    bool containsNearbyAlmostDuplicate(vector<int>& nums, int k,int t) 
    {
        int len=nums.size();
        vector<pair<long,long> >tmp;
        for(int i=0;i<len;i++)
        {
            tmp.push_back(make_pair(nums[i],i));
        }
        cout<<"temp: ";
        for(auto tt:tmp)
        {
            cout<<tt.first;
        }
        sort(tmp.begin(),tmp.end(),cmp);
        for(int i=0;i<len;i++)
        {
            int j=i+1;
            while(abs(tmp[i].first-tmp[j].first)<=t && j<len)
            {
                if(abs(tmp[i].second-tmp[j].second)<=k)
                    return true;
                j++;
            }
        }
        return false;
    }  
};

231 2的幂

给定一个整数，编写一个函数来判断它是否是 2 的幂次方。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
示例 1:
输入: 1
输出: true
解释: 20 = 1
示例 2:
输入: 16
输出: true
解释: 24 = 16
示例 3:
输入: 218
输出: false

法1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    bool isPowerOfTwo(int n) 
    {
        if(n<0) return false;
        int cnt=0;
        while(n)
        {
            cnt=cnt+(n&1);
            n=n>>1;
        }
        return cnt==1;
    }
};

万能法

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    bool isPowerOfTwo(int n) 
    {
        while(n && n%2==0)
        {
            n=n/2;
        }
        return n==1;
    }
};

326 3的幂

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    bool isPowerOfThree(int n) 
    {
        while(n && n%3==0)
        {
            n=n/3;
        }
        return n==1;
    }
};

342 4的幂

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    bool isPowerOfFour(int n) 
    {
        while(n && n%4==0)
        {
            n=n/4;
        }
        return n==1;
    }
};

237 删除链表中的节点

请编写一个函数，使其可以删除某个链表中给定的（非末尾）节点，你将只被给定要求被删除的节点。

现有一个链表 – head = [4,5,1,9]，它可以表示为:
4 -> 5 -> 1 -> 9

1
2
3
4
5
6
7
8
9
10
示例 1:
输入: head = [4,5,1,9], node = 5
输出: [4,1,9]
解释: 给定你链表中值为 5 的第二个节点，那么在调用了你的函数之后，该链表应变为 4 -> 1 -> 9.
示例 2:
输入: head = [4,5,1,9], node = 1
输出: [4,5,9]
解释: 给定你链表中值为 1 的第三个节点，那么在调用了你的函数之后，该链表应变为 4 -> 5 -> 9.

说明:

  • 链表至少包含两个节点。
  • 链表中所有节点的值都是唯一的。
  • 给定的节点为非末尾节点并且一定是链表中的一个有效节点。
  • 不要从你的函数中返回任何结果。

因为题目给的是删除节点，那说明这个节点可以舍弃了，我们把下一个节点的值拷贝给当前要删除的节点，再删除下一个节点。
大致过程如下（删除3）：

1
2
3
1->2->3->4->5 
1->2->4->4->5 
1->2->4->5

这题太骚了：用覆盖的方法

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    void deleteNode(ListNode* node) 
    {
        node->val=node->next->val;
        ListNode* temp=node->next;
        node->next=temp->next;
        delete temp;
    }
};

203 删除链表中的节点

删除链表中等于给定值 val 的所有节点。

示例:

1
2
输入: 1->2->6->3->4->5->6, val = 6
输出: 1->2->3->4->5

方法1：和上面那题（237）类似的思路，删除目标节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        ListNode *dummy = new ListNode(-1), *pre = dummy;
        dummy->next = head;
        while (pre->next) {
            if (pre->next->val == val) {
                ListNode *t = pre->next;
                pre->next = t->next;
                t->next = NULL;
                delete t;
            } else {
                pre = pre->next;
            }
        }
        return dummy->next;
    }
};

经典方法：跳过目标节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) 
    {
        ListNode* dummy=new ListNode(-1);
        dummy->next=head;
        ListNode* pre=dummy;
        ListNode* cur=pre->next;
        while(cur)
        {
            if(cur->val!=val)
            {
                pre=cur;
                cur=cur->next;
            }
            else
            {
                pre->next=cur->next;
                cur=pre->next;
            }
        }
        
        return dummy->next;
    }
};

876 链表的中间结点

给定一个带有头结点 head 的非空单链表，返回链表的中间结点。

如果有两个中间结点，则返回第二个中间结点。

1
2
3
4
5
6
7
8
9
10
11
12
示例 1：
输入：[1,2,3,4,5]
输出：此列表中的结点 3 (序列化形式：[3,4,5])
返回的结点值为 3 。 (测评系统对该结点序列化表述是 [3,4,5])。
注意，我们返回了一个 ListNode 类型的对象 ans，这样：
ans.val = 3, ans.next.val = 4, ans.next.next.val = 5, 以及 ans.next.next.next = NULL.
示例 2：
输入：[1,2,3,4,5,6]
输出：此列表中的结点 4 (序列化形式：[4,5,6])
由于该列表有两个中间结点，值分别为 3 和 4，我们返回第二个结点。

代码:和 109类似的套路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    ListNode* middleNode(ListNode* head) 
    {
        if(head==NULL || head->next==NULL)
            return head;
        ListNode* fast=head->next->next;
        ListNode* slow=head;
        while(fast && fast->next)
        {
            fast=fast->next->next;
            slow=slow->next;
        }
        return slow->next;
    }
};

205 同构字符串

给定两个字符串 s 和 t，判断它们是否是同构的。

如果 s 中的字符可以被替换得到 t ，那么这两个字符串是同构的。

所有出现的字符都必须用另一个字符替换，同时保留字符的顺序。两个字符不能映射到同一个字符上，但字符可以映射自己本身。

1
2
3
4
5
6
7
8
9
10
11
12
示例 1:
输入: s = "egg", t = "add"
输出: true
示例 2:
输入: s = "foo", t = "bar"
输出: false
示例 3:
输入: s = "paper", t = "title"
输出: true

说明:

  • 你可以假设 s 和 t 具有相同的长度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    bool isIsomorphic(string s, string t) 
    {
        map<char,int> char_m1;
        map<char,int> char_m2;
        for(int i=0;i<s.size();i++)
        {
            if(char_m1[s[i]]!=char_m2[t[i]]) return false;
            char_m1[s[i]]=i+1;//原来我是char_m1[s[i]]++;这样只能会把“aba”和“aab”认为是同构，实际上这里丢失了位置对应的信息
            char_m2[t[i]]=i+1;
        }
        return true;
    }
};

739. 每日温度

题目描述提示帮助提交记录社区讨论阅读解答
根据每日 气温 列表，请重新生成一个列表，对应位置的输入是你需要再等待多久温度才会升高的天数。如果之后都不会升高，请输入 0 来代替。

例如，给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73]，你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。

提示：气温 列表长度的范围是 [1, 30000]。每个气温的值的都是 [30, 100] 范围内的整数。

分析：我的思路很简单，遍历每一个元素，对某一个元素来说，找到第一个大于它的数，此时：如果此时的是小于数组的size的，直接push_back(j-i),否则push 0.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<int> dailyTemperatures(vector<int>& temperatures) 
    {
        vector<int> res;
        for(int i=0;i<temperatures.size();i++)
        {
            int j=i+1;
            while(temperatures[j]<=temperatures[i])
            {
                j++;
            }
            if(j<temperatures.size())
            {
                res.push_back(j-i);
            }
            else
            {
                res.push_back(0);
            }
        }
        return res;
    }
};

496 下一个更大元素 I

给定两个没有重复元素的数组 nums1 和 nums2 ，其中nums1 是 nums2 的子集。找到 nums1 中每个元素在 nums2 中的下一个比其大的值。

nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在，对应位置输出-1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
示例 1:
输入: nums1 = [4,1,2], nums2 = [1,3,4,2].
输出: [-1,3,-1]
解释:
    对于num1中的数字4，你无法在第二个数组中找到下一个更大的数字，因此输出 -1。
    对于num1中的数字1，第二个数组中数字1右边的下一个较大数字是 3。
    对于num1中的数字2，第二个数组中没有下一个更大的数字，因此输出 -1。
示例 2:
输入: nums1 = [2,4], nums2 = [1,2,3,4].
输出: [3,-1]
解释:
    对于num1中的数字2，第二个数组中的下一个较大数字是3。
    对于num1中的数字4，第二个数组中没有下一个更大的数字，因此输出 -1。

注意:

  • nums1和nums2中所有元素是唯一的。
  • nums1和nums2 的数组大小都不超过1000。

和上一题的套路有点像

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    vector<int> nextGreaterElement(vector<int>& findNums, vector<int>& nums) 
    {
        vector<int> res(findNums.size(),-1);
        for(int i=0;i<findNums.size();i++)
        {
            int j=0;
            while(findNums[i]!=nums[j] && j<nums.size())
            {
                j++;
            }
            int z=j+1;
            while(nums[z]<=nums[j])
            {
                z++;
            }
            if(z<nums.size())
            {
                res[i]=nums[z];
            }
        }
        return res;
    }
};

503 下一个更大元素 II

给定一个循环数组（最后一个元素的下一个元素是数组的第一个元素），输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1。

示例 1:

1
2
3
4
5
输入: [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2；
数字 2 找不到下一个更大的数； 
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。

注意: 输入数组的长度不会超过 10000。

分析：依次遍历每一个元素。由于数组是循环的，所以先从前面往后面找第一个比它大的数字，如果找不到，就要那么就要从头开始找，第一个比它大的数字。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    vector<int> nextGreaterElements(vector<int>& nums) 
    {
        vector<int> res(nums.size(),-1);
        if(nums.size()==0) return res;
        int j=0;
        while(nums[j]<=nums[nums.size()-1])
        {
            j++;
        }
        if(j<nums.size()) res[nums.size()-1]=nums[j];
        for(int i=0;i<nums.size();i++)
        {
            j=i+1;
            while(nums[i]>=nums[j])
            {
                j++;
            }
            if(j<nums.size()) res[i]=nums[j];
            else//说明顺着没找到，那么就要从头开始找，第一个比它大的数字
            {
                int j=0;
                while(nums[j]<=nums[i]) j++;
                if(j<nums.size()) res[i]=nums[j];
            }
        }
        return res;
    }
};

556 下一个更大元素 III

给定一个32位正整数 n，你需要找到最小的32位整数，其与 n 中存在的位数完全相同，并且其值大于n。如果不存在这样的32位整数，则返回-1。

1
2
3
4
5
6
7
8
示例 1:
输入: 12
输出: 21
示例 2:
输入: 21
输出: -1

这道题给了我们一个数字，让我们对各个位数重新排序，求出刚好比给定数字大的一种排序，如果不存在就返回-1。这道题给的例子的数字都比较简单，我们来看一个复杂的，比如12443322，这个数字的重排序结果应该为13222344，如果我们仔细观察的话会发现数字变大的原因是左数第二位的2变成了3，细心的童鞋会更进一步的发现后面的数字由降序变为了升序，这也不难理解，因为我们要求刚好比给定数字大的排序方式。那么我们再观察下原数字，看看2是怎么确定的，我们发现，如果从后往前看的话，2是第一个小于其右边位数的数字，因为如果是个纯降序排列的数字，做任何改变都不会使数字变大，直接返回-1。知道了找出转折点的方法，再来看如何确定2和谁交换，这里2并没有跟4换位，而是跟3换了，那么如何确定的3？其实也是从后往前遍历，找到第一个大于2的数字交换，然后把转折点之后的数字按升序排列就是最终的结果了。最后记得为防止越界要转为长整数型，然后根据结果判断是否要返回-1即可.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int nextGreaterElement(int n) 
    {
        string s=to_string(n);
        int len=s.size()-1;
        int i=len;
        for(;i>0;i--)
        {
            if(s[i-1]<s[i]) break;
        }
        if(i==0) return -1;
        for(int j=len;j>=i;j--)
        {
            if(s[j]>s[i-1])
            {
                swap(s[j],s[i-1]);
                break;
            }
        }
        sort(s.begin()+i,s.end());
        long long res=stoll(s);
        return res>INT_MAX? -1:res;
    }
};

268 缺失数字

给定一个包含 0, 1, 2, …, n 中 n 个数的序列，找出 0 .. n 中没有出现在序列中的那个数。

1
2
3
4
5
6
7
8
示例 1:
输入: [3,0,1]
输出: 2
示例 2:
输入: [9,6,4,2,3,5,7,0,1]
输出: 8

说明:

  • 你的算法应具有线性时间复杂度。你能否仅使用额外常数空间来实现?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int missingNumber(vector<int>& nums) 
    {
        int len=nums.size();
        map<int,int> m;
        int res=0;
        for(int i=0;i<len;i++)   
        {
            m[nums[i]]++;
        }
        for(int i=0;i<=len;i++)
        {
            if(--m[i]<0)
            {
              res=i;
            }
        }
        return res;
    }
};

113 路径总和 II

给定一个二叉树和一个目标和，找到所有从根节点到叶子节点路径总和等于给定目标和的路径。

说明: 叶子节点是指没有子节点的节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
示例:
给定如下二叉树，以及目标和 sum = 22，
              5
             / \
            4   8
           /   / \
          11  13  4
         /  \    / \
        7    2  5   1
返回:
[
   [5,4,11,2],
   [5,8,4,5]
]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    vector<vector<int>> pathSum(TreeNode* root, int sum) {
        vector<vector<int> >result;
        vector<int> path;
        int path_sum=0;
        preorder(root,path_sum,sum,path,result);
        return result;
    }
private:
    void preorder(TreeNode* node, int &path_sum,int sum,vector<int> &path,vector<vector<int> > &result)
    {
        if(!node)
        {
            return;
        }
        path_sum=path_sum+node->val;
        path.push_back(node->val);
        if(sum==path_sum && !node->left && !node->right)
        {
            result.push_back(path);
        }
        if(node->left) preorder(node->left,path_sum,sum,path,result);
        if(node->right) preorder(node->right,path_sum,sum,path,result);
        path_sum=path_sum-node->val;
        path.pop_back();        
    }
};

257 二叉树的所有路径

题目描述提示帮助提交记录社区讨论阅读解答
给定一个二叉树，返回所有从根节点到叶子节点的路径。

说明:

  • 叶子节点是指没有子节点的节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
示例:
输入:
   1
 /   \
2     3
 \
  5
输出: ["1->2->5", "1->3"]
解释: 所有根节点到叶子节点的路径为: 1->2->5, 1->3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    vector<string> binaryTreePaths(TreeNode* root) 
    {
        vector<string> res;
        if(!root) return res;
        preorder(root,to_string(root->val),res);
        return res;
    }
private:
    void preorder(TreeNode* root,string path,vector<string> &res)
    {
        if(!root) return;
        if(!root->left && !root->right)//说明是叶子节点
        {
            res.push_back(path);
        }
        if(root->left) preorder(root->left,path+"->"+to_string(root->left->val),res);
        if(root->right) preorder(root->right,path+"->"+to_string(root->right->val),res);
        
    }
};

437 路径总和 III

给定一个二叉树，它的每个结点都存放着一个整数值。

找出路径和等于给定数值的路径总数。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

二叉树不超过1000个节点，且节点数值范围是 [-1000000,1000000] 的整数。

示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8
      10
     /  \
    5   -3
   / \    \
  3   2   11
 / \   \
3  -2   1
返回 3。和等于 8 的路径有:
1.  5 -> 3
2.  5 -> 2 -> 1
3.  -3 -> 11

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int pathSum(TreeNode* root, int sum) {
        int res = 0;
        vector<TreeNode*> out;
        helper(root, sum, 0, out, res);
        return res;
    }
    void helper(TreeNode* node, int sum, int curSum, vector<TreeNode*>& out, int& res) {
        if (!node) return;
        curSum += node->val;
        out.push_back(node);
        if (curSum == sum) ++res;
        int t = curSum;
        for (int i = 0; i < out.size() - 1; ++i) {
            t -= out[i]->val;
            if (t == sum) ++res;
        }
        helper(node->left, sum, curSum, out, res);
        helper(node->right, sum, curSum, out, res);
        out.pop_back();
    }
};

415 字符串相加

给定两个字符串形式的非负整数 num1 和num2 ，计算它们的和。

注意：

  • num1 和num2 的长度都小于 5100.
  • num1 和num2 都只包含数字 0-9.
  • num1 和num2 都不包含任何前导零。
  • 你不能使用任何內建 BigInteger 库， 也不能直接将输入的字符串转换为整数形式。

之前LeetCode出过几道类似的题目，比如 67 二进制求和，还有 2 链表相加,和 258 各位相加 基本思路很类似，都是一位一位相加，然后算和算进位，最后根据进位情况看需不需要补一个高位

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    string addStrings(string num1, string num2) 
    {
        string res;
        int i=num1.size()-1;
        int j=num2.size()-1;
        int sum=0,carry=0;
        while(i>=0 || j>=0)
        {
            int a= i>=0? num1[i--]-'0' : 0;
            int b= j>=0? num2[j--]-'0' : 0;
            sum=carry+a+b;
            res.insert(res.begin(),sum%10+'0');
            carry=sum/10;
        }
        return carry==1? '1'+res : res;
    }
};

我之前 2，67 题不是按照这题的代码结构写的，现在重写。

2 链表相加

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    ListNode *addTwoNumbers(ListNode *l1, ListNode *l2) {
        ListNode *res = new ListNode(-1);
        ListNode *cur = res;
        int carry = 0;
        while (l1 || l2) {
            int n1 = l1 ? l1->val : 0;
            int n2 = l2 ? l2->val : 0;
            int sum = n1 + n2 + carry;
            carry = sum / 10;
            cur->next = new ListNode(sum % 10);
            cur = cur->next;
            if (l1) l1 = l1->next;
            if (l2) l2 = l2->next;
        }
        if (carry) cur->next = new ListNode(1);
        return res->next;
    }
};

67 二进制求和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    string addBinary(string a, string b) {
        string res = "";
        int m = a.size() - 1, n = b.size() - 1, carry = 0;
        while (m >= 0 || n >= 0) {
            int p = m >= 0 ? a[m--] - '0' : 0;
            int q = n >= 0 ? b[n--] - '0' : 0;
            int sum = p + q + carry;
            res = to_string(sum % 2) + res;
            carry = sum / 2;
        }
        return carry == 1 ? "1" + res : res;
    }
};

43 字符串相乘

给定两个以字符串形式表示的非负整数 num1 和 num2，返回 num1 和 num2 的乘积，它们的乘积也表示为字符串形式。

1
2
3
4
5
6
7
8
示例 1:
输入: num1 = "2", num2 = "3"
输出: "6"
示例 2:
输入: num1 = "123", num2 = "456"
输出: "56088"

说明：

  • num1 和 num2 的长度小于110。
  • num1 和 num2 只包含数字 0-9。
  • num1 和 num2 均不以零开头，除非是数字 0 本身。
  • 不能使用任何标准库的大数类型（比如 BigInteger）或直接将输入转换为整数来处理。

分析：
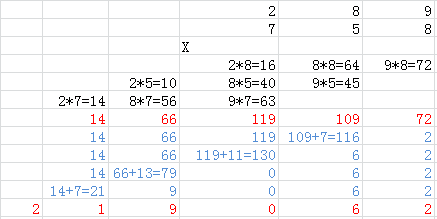
首先我们把每一位相乘，得到一个没有进位的临时结果，如图中中间的一行红色数字就是临时结果，然后把临时结果从低位起依次进位。对于一个m位整数乘以n位整数的结果，最多只有m+n位。

这道题让我们求两个字符串数字的相乘，输入的两个数和返回的数都是以字符串格式储存的，这样做的原因可能是这样可以计算超大数相乘，可以不受int或long的数值范围的约束，那么我们该如何来计算乘法呢，我们小时候都学过多位数的乘法过程，都是每位相乘然后错位相加，那么这里就是用到这种方法，把错位相加后的结果保存到一个一维数组中，然后分别每位上算进位，最后每个数字都变成一位，然后要做的是去除掉首位0，最后把每位上的数字按顺序保存到结果中即可。


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    string multiply(string num1, string num2) 
    {
        string res;
        int n1 = num1.size(), n2 = num2.size();
        int k = n1 + n2 - 2, carry = 0;
        vector<int> v(n1 + n2, 0);
        for (int i = 0; i < n1; ++i) 
        {
            for (int j = 0; j < n2; ++j) 
            {
                v[k - i - j] += (num1[i] - '0') * (num2[j] - '0');
            }
        }
        for (int i = 0; i < n1 + n2; ++i) //处理进位
        {
            v[i] += carry;
            carry = v[i] / 10;
            v[i] %= 10;
        }
        int i = n1 + n2 - 1;
        while (v[i] == 0) --i;//去掉乘积的前导0
        if (i < 0) return "0";//注意乘积为0的特殊情况
        while (i >= 0) res.push_back(v[i--] + '0');
        return res;
    }
};

202 快乐数

编写一个算法来判断一个数是不是“快乐数”。

一个“快乐数”定义为：对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和，然后重复这个过程直到这个数变为 1，也可能是无限循环但始终变不到 1。如果可以变为 1，那么这个数就是快乐数。

示例:

1
2
3
4
5
6
7
输入: 19
输出: true
解释: 
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1

这道题，很容易超出时间限制。大神的做法：我们可以用set来记录所有出现过的数字，然后每出现一个新数字，在set中查找看是否存在，若不存在则加入表中，若存在则跳出循环，并且判断此数是否为1，若为1返回true，不为1返回false。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    bool isHappy(int n)
    {
        set<int> s;
        while(n!=1)
        {
            int t=0;
            while(n)
            {
                t +=(n%10)*(n%10);
                n=n/10;
            }
            n=t;
            if(s.count(n)) break;
            else s.insert(n);            
        }
        return n==1;
    }
};

263. 丑数

编写一个程序判断给定的数是否为丑数。

丑数就是只包含质因数 2, 3, 5 的正整数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
示例 1:
输入: 6
输出: true
解释: 6 = 2 × 3
示例 2:
输入: 8
输出: true
解释: 8 = 2 × 2 × 2
示例 3:
输入: 14
输出: false 
解释: 14 不是丑数，因为它包含了另外一个质因数 7。

说明：

  • 1 是丑数。
  • 输入不会超过 32 位有符号整数的范围: [−231, 231 − 1]。

输入不会超过 32 位有符号整数的范围: [−231, 231 − 1]。
我习惯性写成下面的代码，少了else,那么它就会一行一行往下走。错错错

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    bool isUgly(int n) 
    {
         while(n>=2)
         {
             if(n%2==0) n=n/2;
             if(n%3==0) n=n/3;
             if(n%5==0) n=n/5;
             else return false;
         }
        return n==1;
    }
};

正确的写法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    bool isUgly(int n) 
    {
         while(n>=2)
         {
             if(n%2==0) n=n/2;
             else if(n%3==0) n=n/3;
             else if(n%5==0) n=n/5;
             else return false;
         }
        return n==1;
    }
};

72 编辑距离

给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

  • 插入一个字符
  • 删除一个字符
  • 替换一个字符
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    示例 1:
    输入: word1 = "horse", word2 = "ros"
    输出: 3
    解释: 
    horse -> rorse (将 'h' 替换为 'r')
    rorse -> rose (删除 'r')
    rose -> ros (删除 'e')
    示例 2:
    输入: word1 = "intention", word2 = "execution"
    输出: 5
    解释: 
    intention -> inention (删除 't')
    inention -> enention (将 'i' 替换为 'e')
    enention -> exention (将 'n' 替换为 'x')
    exention -> exection (将 'n' 替换为 'c')
    exection -> execution (插入 'u')

分析：动态规划题。我觉得还是那位大神牛逼，能把别人认为那么难的问题，一下解释的那么好，顿时开光。题目关键是你要确定好状态变量。这里我们用dp[i][j]来表示word1的前i个字符串变换到word2的前j个字符串的最少操作数。那么我们思考前0个字符串到前j个字符串的解，有几个呢？答案是有j个。请看下图：

image

可以把可以把前0个字符串用空集来表示，空集到空集自然不用操作。空集到任何数量(设长度为j)的字符串的操作数就是j(就是把j个元素都作 插入 操作。）这样我们就处理好了边界。对于非边界呢，可以观察到，如果word1[i]=word2[j],那么说明dp[i][j]和（word1前i-1个）=>(word2前j-1个) 相等。其他的情况就是看dp[i][j]的相邻位置哪个更小，取最小的，然后+1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    int minDistance(string word1, string word2) 
    {
        int n1=word1.size();
        int n2=word2.size();
        int dp[n1+1][n2+1];
        for(int i=0;i<=n1;i++)
        {
            dp[i][0]=i;
        }
        for(int i=0;i<=n2;i++)
        {
            dp[0][i]=i;
        }
        for(int i=1;i<=n1;i++)
        {
            for(int j=1;j<=n2;j++)
            {
                if(word1[i-1]==word2[j-1])
                {
                    dp[i][j]=dp[i-1][j-1];
                    
                }
                else
                {
                    dp[i][j]=min(dp[i-1][j-1],min(dp[i-1][j],dp[i][j-1]))+1;
                }
            }
        }
        return dp[n1][n2];
    }
};

583. 两个字符串的删除操作

给定两个单词 word1 和 word2，找到使得 word1 和 word2 相同所需的最小步数，每步可以删除任意一个字符串中的一个字符。

1
2
3
4
5
示例 1:
输入: "sea", "eat"
输出: 2
解释: 第一步将"sea"变为"ea"，第二步将"eat"变为"ea"

说明:

  • 给定单词的长度不超过500。
  • 给定单词中的字符只含有小写字母。

分析：
这一题和上一题【编辑距离】其实是一样的，用dp[i][j]来表示word1前i个字符变换到word2前j个字符的最少操作数。只不过没有插入操作，也就不能考虑那个dp[i-1][j-1]了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    int minDistance(string word1, string word2) 
    {
        int n1=word1.size();
        int n2=word2.size();
        int dp[n1+1][n2+1];
        for(int i=0;i<=n1;i++)
        {
            dp[i][0]=i;
        }
        for(int i=0;i<=n2;i++)
        {
            dp[0][i]=i;
        }
        for(int i=1;i<=n1;i++)
        {
            for(int j=1;j<=n2;j++)
            {
                if(word1[i-1]==word2[j-1])
                {
                    dp[i][j]=dp[i-1][j-1];
                    
                }
                else
                {
                    dp[i][j]=min(dp[i-1][j],dp[i][j-1])+1;
                }
            }
        }
        return dp[n1][n2];    
    }
};

289 生命游戏（回到目录）

根据百度百科，生命游戏，简称为生命，是英国数学家约翰·何顿·康威在1970年发明的细胞自动机。

给定一个包含 m × n 个格子的面板，每一个格子都可以看成是一个细胞。每个细胞具有一个初始状态 live（1）即为活细胞， 或 dead（0）即为死细胞。每个细胞与其八个相邻位置（水平，垂直，对角线）的细胞都遵循以下四条生存定律：

如果活细胞周围八个位置的活细胞数少于两个，则该位置活细胞死亡；
如果活细胞周围八个位置有两个或三个活细胞，则该位置活细胞仍然存活；
如果活细胞周围八个位置有超过三个活细胞，则该位置活细胞死亡；
如果死细胞周围正好有三个活细胞，则该位置死细胞复活；
根据当前状态，写一个函数来计算面板上细胞的下一个（一次更新后的）状态。下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的，其中细胞的出生和死亡是同时发生的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
示例:
输入: 
[
  [0,1,0],
  [0,0,1],
  [1,1,1],
  [0,0,0]
]
输出: 
[
  [0,0,0],
  [1,0,1],
  [0,1,1],
  [0,1,0]
]

由于题目中要求我们用置换方法in-place来解题，所以我们就不能新建一个相同大小的数组，那么我们只能更新原有数组，但是题目中要求所有的位置必须被同时更新，但是在循环程序中我们还是一个位置一个位置更新的，那么当一个位置更新了，这个位置成为其他位置的neighbor时，我们怎么知道其未更新的状态呢，我们可以使用状态机转换：

状态0： 死细胞转为死细胞

状态1： 活细胞转为活细胞

状态2： 活细胞转为死细胞

状态3： 死细胞转为活细胞

最后我们对所有状态对2取余，那么状态0和2就变成死细胞，状态1和3就是活细胞，达成目的。我们先对原数组进行逐个扫描，对于每一个位置，扫描其周围八个位置，如果遇到状态1或2，就计数器累加1，扫完8个邻居，如果少于两个活细胞或者大于三个活细胞，而且当前位置是活细胞的话，标记状态2，如果正好有三个活细胞且当前是死细胞的话，标记状态3。完成一遍扫描后再对数据扫描一遍，对2取余变成我们想要的结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    void gameOfLife(vector<vector<int>>& board) 
    {
        int m=board.size();
        int n=board[0].size();
        if(m==0 || n==0) return;
        vector<vector<int> > dirs={{-1,0},{1,0},{0,-1},{0,1},{-1,-1},{-1,1},{1,-1},{1,1}};
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                int cnt=0;//记录(i,j)点周围8个点的活细胞数量
                for(auto dir:dirs)
                {
                    int x=dir[0]+i,y=dir[1]+j;
                    if(x>=0 && x<m && y>=0 && y<n && (board[x][y]==1 || board[x][y]==2)) 
                    {
                        cnt++;
                    }
                }
                if(board[i][j]==1 && (cnt<2 || cnt>3)) board[i][j]=2;//我这样写不会引起歧义
                else if(board[i][j]==0 && cnt==3) board[i][j]=3;
            }
        }
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                board[i][j] %=2;
            }
        }
    }
};

383 赎金信（回到目录）

给定一个赎金信 (ransom) 字符串和一个杂志(magazine)字符串，判断第一个字符串ransom能不能由第二个字符串magazines里面的字符构成。如果可以构成，返回 true ；否则返回 false。

(题目说明：为了不暴露赎金信字迹，要从杂志上搜索各个需要的字母，组成单词来表达意思。)

注意：

你可以假设两个字符串均只含有小写字母。

1
2
3
canConstruct("a", "b") -> false
canConstruct("aa", "ab") -> false
canConstruct("aa", "aab") -> true

老套路，哈希统计出现的次数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    bool canConstruct(string ransomNote, string magazine) 
    {
        map<int,int> m;
        for(auto c:magazine)
        {
            m[c]++;
        }
        for(auto c:ransomNote)
        {
            if(--m[c]<0)
                return false;
        }
        return true;
    }
};

387 字符串中的第一个唯一字符（回到目录）

给定一个字符串，找到它的第一个不重复的字符，并返回它的索引。如果不存在，则返回 -1。

案例:

1
2
3
4
5
s = "leetcode"
返回 0.
s = "loveleetcode",
返回 2.

老套路了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int firstUniqChar(string s) 
    {
        if(s.empty()) return -1;
        map<int,int> m;
        for(char c:s)
        {
            m[c]++;
        }
        int i=0;
        for(;i<s.size();i++)
        {
            if(m[s[i]] ==1)
                break;
        }
        return i<s.size()? i:-1;
    }
};

451 根据字符出现频率排序（回到目录）

给定一个字符串，请将字符串里的字符按照出现的频率降序排列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
示例 1:
输入:
"tree"
输出:
"eert"
解释:
'e'出现两次，'r'和't'都只出现一次。
因此'e'必须出现在'r'和't'之前。此外，"eetr"也是一个有效的答案。
示例 2:
输入:
"cccaaa"
输出:
"cccaaa"
解释:
'c'和'a'都出现三次。此外，"aaaccc"也是有效的答案。
注意"cacaca"是不正确的，因为相同的字母必须放在一起。
示例 3:
输入:
"Aabb"
输出:
"bbAa"
解释:
此外，"bbaA"也是一个有效的答案，但"Aabb"是不正确的。

注意’A’和’a’被认为是两种不同的字符。

这道题，比较简单，主要是重写cmp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
bool cmp(pair<char,int> &a,pair<char,int> &b)
    {
        return (a.second>b.second || a.second==b.second && a.first<b.first);
    }
class Solution {
public:
    string frequencySort(string s) 
    {
        vector<pair<char,int> > p;
        string res;
        map<char,int> m;
        for(int i=0;i<s.size();i++)
        {
            m[s[i]]++;
        }
        for(int i=0;i<s.size();i++)
        {
            p.push_back(make_pair(s[i],m[s[i]]));
        }
        sort(p.begin(),p.end(),cmp);
        for(auto item:p)
        {
            res.push_back(item.first);
        }
        return res;
    }
};

347 前K个高频元素（回到目录）

给定一个非空的整数数组，返回其中出现频率前 k 高的元素。

1
2
3
4
5
6
7
8
示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
示例 2:
输入: nums = [1], k = 1
输出: [1]

说明：

  • 你可以假设给定的 k 总是合理的，且 1 ≤ k ≤ 数组中不相同的元素的个数。
  • 你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<int> topKFrequent(vector<int>& nums, int k) 
    {
        priority_queue<pair<int,int> > q;//定义一个pair的最大堆，默认应该是根据第一个参数来排序
        map<int,int> m;
        //set<int,greater<int> > cnt;
        vector<int> res;
        for(int i=0;i<nums.size();i++)
        {
            m[nums[i]]++;
        }
        for(auto a:m)
        {
            q.push(make_pair(a.second,a.first));
        }
        for(int i=0;i<k;i++)
        {
            res.push_back(q.top().second);
            q.pop();
        }
        return res;
    }
};

242 有效的字母异位词（回到目录）

给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的一个字母异位词。

1
2
3
4
5
6
7
8
示例 1:
输入: s = "anagram", t = "nagaram"
输出: true
示例 2:
输入: s = "rat", t = "car"
输出: false

说明:

  • 你可以假设字符串只包含小写字母。

老套路，使用map来统计字符数量是否匹配

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    bool isAnagram(string s, string t) 
    {
        map<char,int> m;
        if(s.size() !=t.size()) return false;
        for(int i=0;i<s.size();i++)
        {
            m[s[i]]++;
        }
        for(int i=0;i<t.size();i++)
        {
            if(--m[t[i]]<0)
            {
                return false;
            }
        }
        return true;
    }
};

438 找到字符串中所有字母异位词（回到目录）

给定一个字符串 s 和一个非空字符串 p，找到 s 中所有是 p 的字母异位词的子串，返回这些子串的起始索引。

字符串只包含小写英文字母，并且字符串 s 和 p 的长度都不超过 20100。

说明：

  • 字母异位词指字母相同，但排列不同的字符串。
  • 不考虑答案输出的顺序。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    示例 1:
    输入:
    s: "cbaebabacd" p: "abc"
    输出:
    [0, 6]
    解释:
    起始索引等于 0 的子串是 "cba", 它是 "abc" 的字母异位词。
    起始索引等于 6 的子串是 "bac", 它是 "abc" 的字母异位词。
     示例 2:
    输入:
    s: "abab" p: "ab"
    输出:
    [0, 1, 2]
    解释:
    起始索引等于 0 的子串是 "ab", 它是 "ab" 的字母异位词。
    起始索引等于 1 的子串是 "ba", 它是 "ab" 的字母异位词。
    起始索引等于 2 的子串是 "ab", 它是 "ab" 的字母异位词。

这道题我也想直接用两个map来做的，但是map不能直接比较，所以就选择了两个vector来模拟哈希表。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {//使用两个map 统计两个string的字符数量
public:
    vector<int> findAnagrams(string s, string p) 
    {
        vector<int> res;
        if(s.empty()) return res;
        vector<int> ss(256,0);//这里的256改为122也可以，只要大于z的ASCII码值就好
        vector<int> pp(256,0);
        for(int i=0;i<p.size();i++)
        {
            ss[s[i]]++;
            pp[p[i]]++;
        }
        if(ss==pp) res.push_back(0);
        for(int i=p.size();i<s.size();i++)
        {
            ss[s[i]]++;
            ss[s[i-p.size()]]--;
            if(ss==pp)
            {
                res.push_back(i-p.size()+1);
            }
        }
        return res;
    }
};

567 字符串的排列（回到目录）

给定两个字符串 s1 和 s2，写一个函数来判断 s2 是否包含 s1 的排列。

换句话说，第一个字符串的排列之一是第二个字符串的子串。

1
2
3
4
5
6
7
8
9
10
11
示例1:
输入: s1 = "ab" s2 = "eidbaooo"
输出: True
解释: s2 包含 s1 的排列之一 ("ba").
 
示例2:
输入: s1= "ab" s2 = "eidboaoo"
输出: False

注意：

  • 输入的字符串只包含小写字母
  • 两个字符串的长度都在 [1, 10,000] 之间

和上面那一题（438）一模一样

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    bool checkInclusion(string s1, string s2) 
    {
        if(s1.empty() || s2.empty()) return false;
        vector<int> m1(256,0),m2(256,0);
        for(int i=0;i<s1.size();i++)
        {
            m1[s1[i]]++;
            m2[s2[i]]++;
        }
        if(m1==m2) return true;
        for(int i=s1.size();i<s2.size();i++)
        {
            m2[s2[i]]++;
            m2[s2[i-s1.size()]]--;
            if(m1==m2) return true;
        }
        return false;
    }
};

234 回文链表（回到目录）

请判断一个链表是否为回文链表。

1
2
3
4
5
6
7
8
示例 1:
输入: 1->2
输出: false
示例 2:
输入: 1->2->2->1
输出: true

关键是找出链表中点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    bool isPalindrome(ListNode* head) 
    {
        if(!head || !head->next) return true;
        ListNode* slow=head;
        ListNode* fast=head;
        stack<int> s;
        s.push(head->val);
        while(fast->next && fast->next->next)//先找到中点以前的节点（含中点），并且把它压入栈中
        {
            slow=slow->next;
            fast=fast->next->next;
            s.push(slow->val);
        }
        if(fast->next==NULL) s.pop();//fast->next==NULL；说明此时的slow是中心位置（即，链表是奇数长度），所以要pop掉
        while(slow->next)
        {
            slow=slow->next;
            int temp=s.top();
            s.pop();
            if(temp!=slow->val)
            {
                return false;
            }
        }
        return true;
    }
};

174. 地下城游戏（回到目录）

一些恶魔抓住了公主（P）并将她关在了地下城的右下角。地下城是由 M x N 个房间组成的二维网格。我们英勇的骑士（K）最初被安置在左上角的房间里，他必须穿过地下城并通过对抗恶魔来拯救公主。

骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下，他会立即死亡。

有些房间由恶魔守卫，因此骑士在进入这些房间时会失去健康点数（若房间里的值为负整数，则表示骑士将损失健康点数）；其他房间要么是空的（房间里的值为 0），要么包含增加骑士健康点数的魔法球（若房间里的值为正整数，则表示骑士将增加健康点数）。

为了尽快到达公主，骑士决定每次只向右或向下移动一步。

编写一个函数来计算确保骑士能够拯救到公主所需的最低初始健康点数。

例如，考虑到如下布局的地下城，如果骑士遵循最佳路径 右 -> 右 -> 下 -> 下，则骑士的初始健康点数至少为 7。

1
2
3
-2 (K)	-3	3
-5	-10	1
10	30	-5 (P)

说明:

  • 骑士的健康点数没有上限。
  • 任何房间都可能对骑士的健康点数造成威胁，也可能增加骑士的健康点数，包括骑士进入的左上角房间以及公主被监禁的右下角房间。

分析：


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int calculateMinimumHP(vector<vector<int>>& dungeon) 
    {
        //int res=0;
        int row=dungeon.size();
        int col=dungeon[0].size();
        vector<vector<int> >dp(row,vector<int>(col,0));
        dp[row-1][col-1]=max(1,1-dungeon[row-1][col-1]);
        for(int j=col-2;j>=0;j--)
        {
            dp[row-1][j]=max(1,dp[row-1][j+1]-dungeon[row-1][j]);
        }
        for(int i=row-2;i>=0;i--)
        {
            dp[i][col-1]=max(1,dp[i+1][col-1]-dungeon[i][col-1]);
        }
        for(int i=row-2;i>=0;i--)
        {
            for(int j=col-2;j>=0;j--)
            {
                int dp_min=min(dp[i+1][j],dp[i][j+1]);
                dp[i][j]=max(1,dp_min-dungeon[i][j]);
            }
        }
        return dp[0][0];

304 二维区域和检索 - 矩阵不可变（回到目录）

给定一个二维矩阵，计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1) ，右下角为 (row2, col2)。

上图子矩阵左上角 (row1, col1) = (2, 1) ，右下角(row2, col2) = (4, 3)，该子矩形内元素的总和为 8。

示例:

1
2
3
4
5
6
7
8
9
10
11
给定 matrix = [
  [3, 0, 1, 4, 2],
  [5, 6, 3, 2, 1],
  [1, 2, 0, 1, 5],
  [4, 1, 0, 1, 7],
  [1, 0, 3, 0, 5]
]
sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class NumMatrix {
public:
    vector<vector<int> > v;
    NumMatrix(vector<vector<int> > matrix) {
        int m = matrix.size();
        if(matrix.empty())
            return ;
        int n = matrix[0].size();
        v= vector<vector<int> > (m, vector<int>(n));
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(i == 0 && j == 0) {
                    v[i][j] = matrix[0][0];
                } else if(i == 0) {
                    v[i][j] = v[i][j-1] + matrix[i][j];
                } else if(j == 0) {
                    v[i][j] = v[i-1][j] + matrix[i][j];
                } else {
                    v[i][j] = v[i-1][j] + v[i][j-1] + matrix[i][j] - v[i-1][j-1];
                }
            }
        }
    }
 
    int sumRegion(int row1, int col1, int row2, int col2) {
        if(row1 == 0 && col1 == 0) {
            return v[row2][col2];
        } else if(row1 == 0) {
            return v[row2][col2] - v[row2][col1-1];
        } else if(col1 == 0) {
            return v[row2][col2] - v[row1-1][col2];
        } else {
            return v[row2][col2] - v[row1-1][col2] - v[row2][col1-1] + v[row1-1][col1-1];
        }
    }
};

300 最长上升子序列（回到目录）

给定一个无序的整数数组，找到其中最长上升子序列的长度。

示例:

1
2
3
输入: [10,9,2,5,3,7,101,18]
输出: 4 
解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) 
    {
        if(nums.size()==0) return 0;
        vector<int> dp(nums.size(),0);
        dp[0]=1;
        int res=1;
        for(int i=1;i<dp.size();i++)
        {
            dp[i]=1;
            if(nums[i]>nums[i-1])
            {
                dp[i]=dp[i-1]+1;
            }
            if(res<dp[i])
            {
                res=dp[i];
            }
            
        }
        return res;
    }
};

338 比特位计数（回到目录）

给定一个非负整数 num。对于 0 ≤ i ≤ num 范围中的每个数字 i ，计算其二进制数中的 1 的数目并将它们作为数组返回。

1
2
3
4
5
6
7
8
示例 1:
输入: 2
输出: [0,1,1]
示例 2:
输入: 5
输出: [0,1,1,2,1,2]

方法：假设构造一颗二叉树，根节点为1，从左到右从上到下分别是1，2，3，4…的二进制，可以发现如下规律：左子树是给根节点在末尾加0，右结点是给根节点在末尾加1，可得10和11；后来，10成为根节点，它左子树是100，右子树是101；11为根节点的树，左子树是110，右子树是111，同样是左边加0，右边加1…也就是当前数为偶数就在左子树，加0；如果当前数是奇数就在右子树，加1。如下图：


1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    vector<int> countBits(int num) 
    {
        vector<int> dp(num+1);
        dp[0]=0;
        for(int i=1;i<=num;i++)
        {
            dp[i]=dp[i>>1]+i%2;
        }
        return dp;
    }
};

279 完全平方数（回到目录）

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, …）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

1
2
3
4
5
6
7
8
9
10
示例 1:
输入: n = 12
输出: 3 
解释: 12 = 4 + 4 + 4.
示例 2:
输入: n = 13
输出: 2
解释: 13 = 4 + 9.

分析：建立一个n+1长度的数组dp，dp[i]表示i这个数构成平方和需要数字的最小个数。
当jxj小于i的时候，temp中保存j从1开始每加1得到的dp[i-jxj] + 1的最小值
当jXj=i的时候，dp[i]的值就直接为1。从2一直到n可以计算出dp[i]的所有值。。
最后return dp[n]的值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int numSquares(int n) {
        vector<int> dp(n+1);
        dp[1] = 1;
        for(int i = 2; i <= n; i++) {
            int temp = 99999999;
            for(int j = 1; j * j <= i; j++) {
                if(j * j == i) {
                    temp = 1;
                    break;
                }
                temp = min(temp, dp[i-j*j] + 1);
            }
            dp[i] = temp;
        }
        return dp[n];
    }
};

91 解码方法

一条包含字母 A-Z 的消息通过以下方式进行了编码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
'A' -> 1
'B' -> 2
...
'Z' -> 26
给定一个只包含数字的非空字符串，请计算解码方法的总数。
示例 1:
输入: "12"
输出: 2
解释: 它可以解码为 "AB"（1 2）或者 "L"（12）。
示例 2:
输入: "226"
输出: 3
解释: 它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6) 。

这道题要求解码方法，跟之前那道 Climbing Stairs 爬梯子问题 非常的相似，但是还有一些其他的限制条件，比如说一位数时不能为0，两位数不能大于26，其十位上的数也不能为0，出去这些限制条件，根爬梯子基本没啥区别，也勉强算特殊的斐波那契数列，当然需要用动态规划Dynamci Programming来解。建立一位dp数组，长度比输入数组长多多2，全部初始化为1，因为斐波那契数列的前两项也为1，然后从第三个数开始更新，对应数组的第一个数。对每个数组首先判断其是否为0，若是将改为dp赋0，若不是，赋上一个dp值，此时相当如加上了dp[i - 1], 然后看数组前一位是否存在，如果存在且满足前一位不是0，且和当前为一起组成的两位数不大于26，则当前dp值加上dp[i - 2], 至此可以看出来跟斐波那契数组的递推式一样，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int numDecodings(string s) {
        if (s.empty() || (s.size() > 1 && s[0] == '0')) return 0;
        vector<int> dp(s.size(), 0);
        dp[0] = 1;
        for (int i = 1; i < dp.size(); ++i) {
            dp[i] = (s[i - 1] == '0') ? 0 : dp[i - 1];
            if (i > 1 && (s[i - 2] == '1' || (s[i - 2] == '2' && s[i - 1] <= '6'))) {
                dp[i] += dp[i - 2];
            }
        }
        return dp.back();
    }
};

96 不同的二叉搜索树（回到目录）

给定一个整数 n，求以 1 … n 为节点组成的二叉搜索树有多少种？

示例:

1
2
3
4
5
6
7
8
9
10
输入: 3
输出: 5
解释:
给定 n = 3, 一共有 5 种不同结构的二叉搜索树:
   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

二分查找树的定义是，左子树节点均小于root，右子树节点均大于root,所以可以用递推的方法，把dp[i]表示i个数能够构成的二叉搜索树的个数.初始化边界值是 dp[0]=1,dp[1]=1,dp[2]=2。
当i>=3的时候，若以j为root结点，dp[j-1]等于root结点左边的j-1个结点能构成的BST个数.
dp[i-j]等于root结点右边i-j个结点能构成的BST个数。因为j+1~i的种数和0~i-j的种数一样，所以就是dp[i-j]所以dp[j-1] * dp[i-j]等于以j为root结点能构成的BST种数
j可以取1~i中的任意一个值，把这些所有计算出来的总数相加就是v[i]的值

1
2
3
4
5
6
7
8
9
10
11
12
                 1                        n = 1
             2        1                   n = 2
            /          \
           1            2
  
1         3     3      2      1           n = 3
 \       /     /      / \      \
  3     2     1      1   3      2
 /     /       \                 \
2     1         2                 3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int numTrees(int n) 
    {
        vector<int> dp(n+1);
        dp[0]=1;
        dp[1]=1;
        dp[2]=2;
        for(int i=3;i<=n;i++)
        {
            for(int j=1;j<=i;j++)
            {
                dp[i] +=dp[i-1]*dp[i-j];
            }
        }
        return dp[n];
    }
};

443 压缩字符串

给定一组字符，使用原地算法将其压缩。

压缩后的长度必须始终小于或等于原数组长度。

数组的每个元素应该是长度为1 的字符（不是 int 整数类型）。

在完成原地修改输入数组后，返回数组的新长度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
示例 1：
输入：
["a","a","b","b","c","c","c"]
输出：
返回6，输入数组的前6个字符应该是：["a","2","b","2","c","3"]
说明：
"aa"被"a2"替代。"bb"被"b2"替代。"ccc"被"c3"替代。
示例 2：
输入：
["a"]
输出：
返回1，输入数组的前1个字符应该是：["a"]
说明：
没有任何字符串被替代。
示例 3：
输入：
["a","b","b","b","b","b","b","b","b","b","b","b","b"]
输出：
返回4，输入数组的前4个字符应该是：["a","b","1","2"]。
说明：
由于字符"a"不重复，所以不会被压缩。"bbbbbbbbbbbb"被“b12”替代。
注意每个数字在数组中都有它自己的位置。

注意：

所有字符都有一个ASCII值在[35, 126]区间内。
1 <= len(chars) <= 1000。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int compress(vector<char>& chars) 
    {
        int cur=0;
        for(int i=0,j=0;i<chars.size();i=j)
        {
            while(j<chars.size() && chars[i]==chars[j]) j++;
            chars[cur++]=chars[i];
            if(j-i==1) continue;
            for(char digit:to_string(j-i))
            {
                chars[cur++]=digit;
            }
        }
        return cur;
    }
};

693 交替位二进制数

给定一个正整数，检查他是否为交替位二进制数：换句话说，就是他的二进制数相邻的两个位数永不相等。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
示例 1:
输入: 5
输出: True
解释:
5的二进制数是: 101
示例 2:
输入: 7
输出: False
解释:
7的二进制数是: 111
示例 3:
输入: 11
输出: False
解释:
11的二进制数是: 1011
 示例 4:
输入: 10
输出: True
解释:
10的二进制数是: 1010

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    bool hasAlternatingBits(int n) 
    {
        //if(n==1) return false;
        int bit=-1;
        while(n>0)
        {
            if(n&1==1)
            {
                if(bit==1) return false;
                bit=1;
            }
            else
            {
            
                if(bit==0) return false;
                bit=0;
            }
            n=n>>1;
        }
        return true;
    }
};
-------------本文结束感谢您的阅读-------------
您的小小鼓励，是我不断更新的强大动力！